Lc回路 微分方程式 - Gan's blog - フォーラム / May 24, 2020 · lc並列回路の過渡現象（直流回路） 2020年5月24日;. 回路方程式の【左辺= 0 】として解が得られる（線形斉次微分方程式の一般解） 2 2 1 0 t t c lr2 1 0 c oo 特性方程式 解の公式を用いて， 2 2 2 12 4 41, 2 l rr rc c §· ¨¸ ©¹ o 根号（ルート）内の符号により，3つのパターンが存在する 2 1 2 r l lc §· ¨¸ ©¹ 3 2 1 2 r l lc. §7.3 線形微分方程式と固有値 線形微分方程式を連立方程式にして解きます．したがって，行列の対角化に 伴う固有値が現れます．始めに，バネで結んだ重りの運動を考えます（摩擦が ある場合とない場合）．次に，それと形式的に同型の電気回路（lcr 回路. 微分方程式 7.1 微分方程式とは 自然科学の基礎方程式は多くの場合、「ある状況のもとで、着目する量がどのように微 小変化するか」を記述する。すなわち、系の状況を指定するいくつかの変数! May 24, 2020 · lc並列回路の過渡現象（直流回路） 2020年5月24日; Telegraphic equation ）とは、波動や信号の伝播を記述する2階の線形偏微分方程式のこと。 分布定数回路 における電流や電圧の分布、導体中の 電磁場 の伝播、減衰のある弦の振動などの現象を記述する。
May 24, 2020 · lc並列回路の過渡現象（直流回路） 2020年5月24日; 微分方程式を用いた解法（lc回路） コイルとコンデンサを直列につないだlc回路を考える。 lc回路も電磁気の知識を使えば微分方程式を立てることができる。 ここでは、交流と直流の両方の場合の微分方程式を考えて解いてみる。 図1 直流のlc回路 直流の場合 Telegraphic equation ）とは、波動や信号の伝播を記述する2階の線形偏微分方程式のこと。 分布定数回路 における電流や電圧の分布、導体中の 電磁場 の伝播、減衰のある弦の振動などの現象を記述する。 §7.3 線形微分方程式と固有値 線形微分方程式を連立方程式にして解きます．したがって，行列の対角化に 伴う固有値が現れます．始めに，バネで結んだ重りの運動を考えます（摩擦が ある場合とない場合）．次に，それと形式的に同型の電気回路（lcr 回路. 微分方程式 7.1 微分方程式とは 自然科学の基礎方程式は多くの場合、「ある状況のもとで、着目する量がどのように微 小変化するか」を記述する。すなわち、系の状況を指定するいくつかの変数!
RC直列回路の過渡現象の解き方 from eleking.net §7.3 線形微分方程式と固有値 線形微分方程式を連立方程式にして解きます．したがって，行列の対角化に 伴う固有値が現れます．始めに，バネで結んだ重りの運動を考えます（摩擦が ある場合とない場合）．次に，それと形式的に同型の電気回路（lcr 回路. Telegraphic equation ）とは、波動や信号の伝播を記述する2階の線形偏微分方程式のこと。 分布定数回路 における電流や電圧の分布、導体中の 電磁場 の伝播、減衰のある弦の振動などの現象を記述する。 微分方程式 7.1 微分方程式とは 自然科学の基礎方程式は多くの場合、「ある状況のもとで、着目する量がどのように微 小変化するか」を記述する。すなわち、系の状況を指定するいくつかの変数! May 24, 2020 · lc並列回路の過渡現象（直流回路） 2020年5月24日; 回路方程式の【左辺= 0 】として解が得られる（線形斉次微分方程式の一般解） 2 2 1 0 t t c lr2 1 0 c oo 特性方程式 解の公式を用いて， 2 2 2 12 4 41, 2 l rr rc c §· ¨¸ ©¹ o 根号（ルート）内の符号により，3つのパターンが存在する 2 1 2 r l lc §· ¨¸ ©¹ 3 2 1 2 r l lc. 微分方程式を用いた解法（lc回路） コイルとコンデンサを直列につないだlc回路を考える。 lc回路も電磁気の知識を使えば微分方程式を立てることができる。 ここでは、交流と直流の両方の場合の微分方程式を考えて解いてみる。 図1 直流のlc回路 直流の場合 そのシートを用いlc回路方程式を解いてみよう。 図3のように、l=0.02,c=0.01,初期電流1(a)の条件でlc回路方程式を解くと、図2の様に共振していることがわかる。共振の周期(t)の理論解は t = 2π√(lc) = 0.028となり、グラフから読み取れる周期と一致している。
微分方程式 7.1 微分方程式とは 自然科学の基礎方程式は多くの場合、「ある状況のもとで、着目する量がどのように微 小変化するか」を記述する。すなわち、系の状況を指定するいくつかの変数!
§7.3 線形微分方程式と固有値 線形微分方程式を連立方程式にして解きます．したがって，行列の対角化に 伴う固有値が現れます．始めに，バネで結んだ重りの運動を考えます（摩擦が ある場合とない場合）．次に，それと形式的に同型の電気回路（lcr 回路. そのシートを用いlc回路方程式を解いてみよう。 図3のように、l=0.02,c=0.01,初期電流1(a)の条件でlc回路方程式を解くと、図2の様に共振していることがわかる。共振の周期(t)の理論解は t = 2π√(lc) = 0.028となり、グラフから読み取れる周期と一致している。 微分方程式を用いた解法（lc回路） コイルとコンデンサを直列につないだlc回路を考える。 lc回路も電磁気の知識を使えば微分方程式を立てることができる。 ここでは、交流と直流の両方の場合の微分方程式を考えて解いてみる。 図1 直流のlc回路 直流の場合 微分方程式 7.1 微分方程式とは 自然科学の基礎方程式は多くの場合、「ある状況のもとで、着目する量がどのように微 小変化するか」を記述する。すなわち、系の状況を指定するいくつかの変数! 回路方程式の【左辺= 0 】として解が得られる（線形斉次微分方程式の一般解） 2 2 1 0 t t c lr2 1 0 c oo 特性方程式 解の公式を用いて， 2 2 2 12 4 41, 2 l rr rc c §· ¨¸ ©¹ o 根号（ルート）内の符号により，3つのパターンが存在する 2 1 2 r l lc §· ¨¸ ©¹ 3 2 1 2 r l lc. May 24, 2020 · lc並列回路の過渡現象（直流回路） 2020年5月24日; Telegraphic equation ）とは、波動や信号の伝播を記述する2階の線形偏微分方程式のこと。 分布定数回路 における電流や電圧の分布、導体中の 電磁場 の伝播、減衰のある弦の振動などの現象を記述する。
微分方程式を用いた解法（lc回路） コイルとコンデンサを直列につないだlc回路を考える。 lc回路も電磁気の知識を使えば微分方程式を立てることができる。 ここでは、交流と直流の両方の場合の微分方程式を考えて解いてみる。 図1 直流のlc回路 直流の場合 そのシートを用いlc回路方程式を解いてみよう。 図3のように、l=0.02,c=0.01,初期電流1(a)の条件でlc回路方程式を解くと、図2の様に共振していることがわかる。共振の周期(t)の理論解は t = 2π√(lc) = 0.028となり、グラフから読み取れる周期と一致している。 回路方程式の【左辺= 0 】として解が得られる（線形斉次微分方程式の一般解） 2 2 1 0 t t c lr2 1 0 c oo 特性方程式 解の公式を用いて， 2 2 2 12 4 41, 2 l rr rc c §· ¨¸ ©¹ o 根号（ルート）内の符号により，3つのパターンが存在する 2 1 2 r l lc §· ¨¸ ©¹ 3 2 1 2 r l lc. §7.3 線形微分方程式と固有値 線形微分方程式を連立方程式にして解きます．したがって，行列の対角化に 伴う固有値が現れます．始めに，バネで結んだ重りの運動を考えます（摩擦が ある場合とない場合）．次に，それと形式的に同型の電気回路（lcr 回路. 微分方程式 7.1 微分方程式とは 自然科学の基礎方程式は多くの場合、「ある状況のもとで、着目する量がどのように微 小変化するか」を記述する。すなわち、系の状況を指定するいくつかの変数!
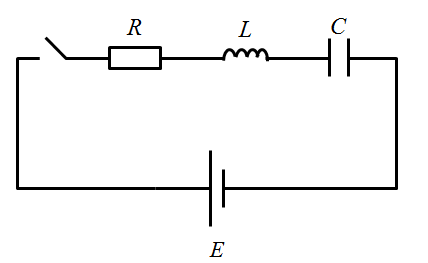なり、 \(RLC\)直並列回路 from den1-tanaoroshi.com 微分方程式 7.1 微分方程式とは 自然科学の基礎方程式は多くの場合、「ある状況のもとで、着目する量がどのように微 小変化するか」を記述する。すなわち、系の状況を指定するいくつかの変数! Telegraphic equation ）とは、波動や信号の伝播を記述する2階の線形偏微分方程式のこと。 分布定数回路 における電流や電圧の分布、導体中の 電磁場 の伝播、減衰のある弦の振動などの現象を記述する。 §7.3 線形微分方程式と固有値 線形微分方程式を連立方程式にして解きます．したがって，行列の対角化に 伴う固有値が現れます．始めに，バネで結んだ重りの運動を考えます（摩擦が ある場合とない場合）．次に，それと形式的に同型の電気回路（lcr 回路. 微分方程式を用いた解法（lc回路） コイルとコンデンサを直列につないだlc回路を考える。 lc回路も電磁気の知識を使えば微分方程式を立てることができる。 ここでは、交流と直流の両方の場合の微分方程式を考えて解いてみる。 図1 直流のlc回路 直流の場合 回路方程式の【左辺= 0 】として解が得られる（線形斉次微分方程式の一般解） 2 2 1 0 t t c lr2 1 0 c oo 特性方程式 解の公式を用いて， 2 2 2 12 4 41, 2 l rr rc c §· ¨¸ ©¹ o 根号（ルート）内の符号により，3つのパターンが存在する 2 1 2 r l lc §· ¨¸ ©¹ 3 2 1 2 r l lc. そのシートを用いlc回路方程式を解いてみよう。 図3のように、l=0.02,c=0.01,初期電流1(a)の条件でlc回路方程式を解くと、図2の様に共振していることがわかる。共振の周期(t)の理論解は t = 2π√(lc) = 0.028となり、グラフから読み取れる周期と一致している。 May 24, 2020 · lc並列回路の過渡現象（直流回路） 2020年5月24日;
そのシートを用いlc回路方程式を解いてみよう。 図3のように、l=0.02,c=0.01,初期電流1(a)の条件でlc回路方程式を解くと、図2の様に共振していることがわかる。共振の周期(t)の理論解は t = 2π√(lc) = 0.028となり、グラフから読み取れる周期と一致している。
Telegraphic equation ）とは、波動や信号の伝播を記述する2階の線形偏微分方程式のこと。 分布定数回路 における電流や電圧の分布、導体中の 電磁場 の伝播、減衰のある弦の振動などの現象を記述する。 微分方程式を用いた解法（lc回路） コイルとコンデンサを直列につないだlc回路を考える。 lc回路も電磁気の知識を使えば微分方程式を立てることができる。 ここでは、交流と直流の両方の場合の微分方程式を考えて解いてみる。 図1 直流のlc回路 直流の場合 微分方程式 7.1 微分方程式とは 自然科学の基礎方程式は多くの場合、「ある状況のもとで、着目する量がどのように微 小変化するか」を記述する。すなわち、系の状況を指定するいくつかの変数! 回路方程式の【左辺= 0 】として解が得られる（線形斉次微分方程式の一般解） 2 2 1 0 t t c lr2 1 0 c oo 特性方程式 解の公式を用いて， 2 2 2 12 4 41, 2 l rr rc c §· ¨¸ ©¹ o 根号（ルート）内の符号により，3つのパターンが存在する 2 1 2 r l lc §· ¨¸ ©¹ 3 2 1 2 r l lc. そのシートを用いlc回路方程式を解いてみよう。 図3のように、l=0.02,c=0.01,初期電流1(a)の条件でlc回路方程式を解くと、図2の様に共振していることがわかる。共振の周期(t)の理論解は t = 2π√(lc) = 0.028となり、グラフから読み取れる周期と一致している。 May 24, 2020 · lc並列回路の過渡現象（直流回路） 2020年5月24日; §7.3 線形微分方程式と固有値 線形微分方程式を連立方程式にして解きます．したがって，行列の対角化に 伴う固有値が現れます．始めに，バネで結んだ重りの運動を考えます（摩擦が ある場合とない場合）．次に，それと形式的に同型の電気回路（lcr 回路.
§7.3 線形微分方程式と固有値 線形微分方程式を連立方程式にして解きます．したがって，行列の対角化に 伴う固有値が現れます．始めに，バネで結んだ重りの運動を考えます（摩擦が ある場合とない場合）．次に，それと形式的に同型の電気回路（lcr 回路. そのシートを用いlc回路方程式を解いてみよう。 図3のように、l=0.02,c=0.01,初期電流1(a)の条件でlc回路方程式を解くと、図2の様に共振していることがわかる。共振の周期(t)の理論解は t = 2π√(lc) = 0.028となり、グラフから読み取れる周期と一致している。 回路方程式の【左辺= 0 】として解が得られる（線形斉次微分方程式の一般解） 2 2 1 0 t t c lr2 1 0 c oo 特性方程式 解の公式を用いて， 2 2 2 12 4 41, 2 l rr rc c §· ¨¸ ©¹ o 根号（ルート）内の符号により，3つのパターンが存在する 2 1 2 r l lc §· ¨¸ ©¹ 3 2 1 2 r l lc. Telegraphic equation ）とは、波動や信号の伝播を記述する2階の線形偏微分方程式のこと。 分布定数回路 における電流や電圧の分布、導体中の 電磁場 の伝播、減衰のある弦の振動などの現象を記述する。 微分方程式を用いた解法（lc回路） コイルとコンデンサを直列につないだlc回路を考える。 lc回路も電磁気の知識を使えば微分方程式を立てることができる。 ここでは、交流と直流の両方の場合の微分方程式を考えて解いてみる。 図1 直流のlc回路 直流の場合
微分方程式を用いた解法（RLC回路） from physics.thick.jp 微分方程式 7.1 微分方程式とは 自然科学の基礎方程式は多くの場合、「ある状況のもとで、着目する量がどのように微 小変化するか」を記述する。すなわち、系の状況を指定するいくつかの変数! 微分方程式を用いた解法（lc回路） コイルとコンデンサを直列につないだlc回路を考える。 lc回路も電磁気の知識を使えば微分方程式を立てることができる。 ここでは、交流と直流の両方の場合の微分方程式を考えて解いてみる。 図1 直流のlc回路 直流の場合 そのシートを用いlc回路方程式を解いてみよう。 図3のように、l=0.02,c=0.01,初期電流1(a)の条件でlc回路方程式を解くと、図2の様に共振していることがわかる。共振の周期(t)の理論解は t = 2π√(lc) = 0.028となり、グラフから読み取れる周期と一致している。 §7.3 線形微分方程式と固有値 線形微分方程式を連立方程式にして解きます．したがって，行列の対角化に 伴う固有値が現れます．始めに，バネで結んだ重りの運動を考えます（摩擦が ある場合とない場合）．次に，それと形式的に同型の電気回路（lcr 回路. May 24, 2020 · lc並列回路の過渡現象（直流回路） 2020年5月24日; 回路方程式の【左辺= 0 】として解が得られる（線形斉次微分方程式の一般解） 2 2 1 0 t t c lr2 1 0 c oo 特性方程式 解の公式を用いて， 2 2 2 12 4 41, 2 l rr rc c §· ¨¸ ©¹ o 根号（ルート）内の符号により，3つのパターンが存在する 2 1 2 r l lc §· ¨¸ ©¹ 3 2 1 2 r l lc. Telegraphic equation ）とは、波動や信号の伝播を記述する2階の線形偏微分方程式のこと。 分布定数回路 における電流や電圧の分布、導体中の 電磁場 の伝播、減衰のある弦の振動などの現象を記述する。
微分方程式 7.1 微分方程式とは 自然科学の基礎方程式は多くの場合、「ある状況のもとで、着目する量がどのように微 小変化するか」を記述する。すなわち、系の状況を指定するいくつかの変数!
§7.3 線形微分方程式と固有値 線形微分方程式を連立方程式にして解きます．したがって，行列の対角化に 伴う固有値が現れます．始めに，バネで結んだ重りの運動を考えます（摩擦が ある場合とない場合）．次に，それと形式的に同型の電気回路（lcr 回路. May 24, 2020 · lc並列回路の過渡現象（直流回路） 2020年5月24日; そのシートを用いlc回路方程式を解いてみよう。 図3のように、l=0.02,c=0.01,初期電流1(a)の条件でlc回路方程式を解くと、図2の様に共振していることがわかる。共振の周期(t)の理論解は t = 2π√(lc) = 0.028となり、グラフから読み取れる周期と一致している。 微分方程式を用いた解法（lc回路） コイルとコンデンサを直列につないだlc回路を考える。 lc回路も電磁気の知識を使えば微分方程式を立てることができる。 ここでは、交流と直流の両方の場合の微分方程式を考えて解いてみる。 図1 直流のlc回路 直流の場合 微分方程式 7.1 微分方程式とは 自然科学の基礎方程式は多くの場合、「ある状況のもとで、着目する量がどのように微 小変化するか」を記述する。すなわち、系の状況を指定するいくつかの変数! 回路方程式の【左辺= 0 】として解が得られる（線形斉次微分方程式の一般解） 2 2 1 0 t t c lr2 1 0 c oo 特性方程式 解の公式を用いて， 2 2 2 12 4 41, 2 l rr rc c §· ¨¸ ©¹ o 根号（ルート）内の符号により，3つのパターンが存在する 2 1 2 r l lc §· ¨¸ ©¹ 3 2 1 2 r l lc. Telegraphic equation ）とは、波動や信号の伝播を記述する2階の線形偏微分方程式のこと。 分布定数回路 における電流や電圧の分布、導体中の 電磁場 の伝播、減衰のある弦の振動などの現象を記述する。
Telegraphic equation ）とは、波動や信号の伝播を記述する2階の線形偏微分方程式のこと。 分布定数回路 における電流や電圧の分布、導体中の 電磁場 の伝播、減衰のある弦の振動などの現象を記述する。 lck. 微分方程式 7.1 微分方程式とは 自然科学の基礎方程式は多くの場合、「ある状況のもとで、着目する量がどのように微 小変化するか」を記述する。すなわち、系の状況を指定するいくつかの変数!
Komentar
Posting Komentar